0x00 接触KMP
第一次接触KMP算法是在大学数据结构课程中,当时就感觉这算法很费解,学了忘,忘了学,乐此不疲,想是自己愚钝,结果发现并非只有我有这种感觉,现在想起来,更多是没对算法背景的原因有系统点的理解,趁最近有点时间,刚好再补习一次。
0x01 KMP背景
KMP是一个字符串匹配的算法,在KMP之前,想想我们如果要查找字符串里是否存在匹配串是怎么做的。
字符串: ABCDABD
匹配串: ABD
| A | B | C | D | A | B | D |
| A | B | D |
匹配到index=2时,’C’!=’D’,导致失配,传统的做法就是在将匹配串右移一位,重新进行匹配
| A | B | C | D | A | B | D |
| A | B | D |
一直匹配到最后
| A | B | C | D | A | B | D |
| A | B | D |
最终匹配串匹配到最后一位,说明能在字符串中找到对应的匹配串,匹配成功。
以上算法比较简单,但性能较差,最坏的情况下需要做(M-N+1)×N次的操作(M为字符串长度,N为匹配串长度)。
0x02 KMP简述
简单来说,KMP之所以能优化性能,是因为在对比过程中通过标记数组来避免了无意义的字符对比,从而直接减少对比次数,提升性能。
比起匹配算法,KMP更重要的是next的计算。
0x03 next的意义
NEXT是针对匹配串进行计算的,先于做字符串匹配前进行计算,当字符串第i位与匹配串第n位失配时,其意义表示
next[n]指示匹配串在失配时应该跳转的位置
跳转后,字符串当前匹配的索引值i不需要变化,只需要继续将字符串第i位与匹配串第(n-next[b])位开始匹配即可。
有了这个NEXT数组,就可以在匹配过程中提前失败失配时的有效跳转距离,避免无效对比。
0x10 生成next数组
既然next数组这么重要,那该如何生成?
0x11 前缀 —— 后缀最大长度
在计算next之前,先理解一个概念,字符串子串的前缀与后缀。
以字符串“ABCABD”为例,其子串前缀与后缀如下:
| 子串 | 前缀 | 后缀 | 最大长度 |
|---|---|---|---|
| A | - | - | 0 |
| AB | A | B | 0 |
| ABC | A,AB | C,BC | 0 |
| ABCA | A,AB,ABC | A,CA,BCA | 1 |
| ABCAB | A,AB,ABC,ABCA | B,AB,CAB,BCAB | 2 |
| ABCABD | A,AB,ABC,ABCA,ABCAB | D,BD,ABD,CABD,BCABD | 0 |
定义如下:
- 子串:字符串的一部分
- 前缀:所有包含首位字符但不包含未位字符的子串
- 后缀:所有包含未位字符但不包含首位字符的子串
- 最大长度:前缀后缀集合内相同子串的最大长度
对于”ABCAB“而言,其对应的最大长度定义为
| A | B | C | A | B | D |
| 0 | 0 | 0 | 1 | 2 | 0 |
其每一位maxLen[n]的意义可以理解为:
第n位字符之前有maxLen[n]个字符与整个字符串的匹配
如n=4,maxLen[4]=2,说明到字符‘B’为止有两个字符与整个字符串匹配,即最后两个”AB“与最开始两个”AB“匹配,长度为2。
0x12 next与前后缀的关系
next数组定义的是当失配时可以跳转的距离,实际上这个距离的另一个含义是
匹配串的前next[n]不再需要对比
回想上一节前后缀的计算方式,是通过找到字符串后面的子串与包含首位字符的子串的最大长度(重点在于子串是从首位字符开始算起的),这样就可以将next与前后缀的计算联立起来了。
再看回这个例子
| A | B | C | A | B | D |
| 0 | 0 | 0 | 1 | 2 | 0 |
假设 “ABCAB” 是匹配串,当n=4(‘B’)失配时,它的最长子串长度为2,其含义为匹配串最开头的2个字符也是”AB”,而实际上,既然此时n已经等于4了,说明n=3时是能够匹配上字符串的,那在失配时就不需要从n=0开始重新匹配,只需要从n=1开始重新匹配就可以了,而第一位的‘A’就不需要重新匹配,省去一次匹配。
于是可以得出,在失配时(设位置为n),
应跳回到失配字符前一个字符的maxLen[n]
即当n=4失败时,n需要回到n=next[3]=1处(‘A’),而此时n=1处因为还是‘B’,依然失配,则再次回到n=next[0]=0的位置处,也就是重新开始(这里明显有优化空间,下述)
如此,我们就可以得出next值了,next等于maxLen一位:
| 字符串 | A | B | C | A | B | D |
| maxLen | 0 | 0 | 0 | 1 | 2 | 0 |
| next | 0 | 0 | 0 | 0 | 1 | 2 |
0x13 next的优化
如下一节所述,当n=4失配时,就算回到n=1的地方,因为p[4]=p[1]=’B’,所以即使n跳回去还没是用,因为字符肯定还是不匹配的,所以此时n应该再跳一级
n=next[next[n]]
0x14 简单串的next口算
上一节只是为了描述next值背后的含义,但实际计算中,我们是不可能这样子把子串的所有前缀后缀穷举然后匹配最长子串的。
以“ABDCABABDAC”串为例,需要分段计算:
- 前几个串的next值为
| 字符串 | A | B | D | C | A | B | A | B | D | A | C |
| next | 0 | 0 | 0 | 0 |
因为next值是需要与前缀子串相关,前缀子串肯定包含首字符,所以当字符不存在首位字符时,其next值直接置为0即可。
- 开始有前缀匹配
| 字符串 | A | B | D | C | A | B | A | B | D | A | C |
| next | 0 | 0 | 0 | 0 | 0 | 2 | 0 | 0 | 0 | 3 | 1 |
| 解释 | k=2 | (1) | (2) | (3) | (4) | (5) | (6) |
分点解析如下:
(1) 这个好理解,当前字符的next表示的是‘A’失配时回去的地方,此时‘A’失配了,那应该整体字符串右移,从头来过(因为首位字符就已经是’A‘了)
(2) 这个值本身其实是1,因为’B‘失配时,此时前面的’A’已经配对成功,应该回到n=1的位置,但基于优化方案,此时回去也没用,所以应该回到n=0的位置,即next[1]的位置
(3) 在这个位置n=6时,应该是要与k=2的值作比较的,但此时失配了,即前面最长的子串长度maxLen为k=2,此时next[n]=k=2
这里的k,其实就是最长子串的匹配索引值(从首位开始),因为此时失配了,再去找最长的子串已经不行了,k值需要回到上一个最长子串匹配的地方,即k=next[k],直到p[k]!=p[n],或k已经到首位字符为止
(4) 当k值重新置位后,p[k]=p[n]=’A’,此时是匹配的,k与n都可以向后移一位,匹配下一个符号
(5) 与(3)是一样的,k此时已经去到3的位置了(‘C’),此时失配,k复位到k=next[k]=0; 另外,与(4)一样,k复位后存在适配的字符(‘A’),k与n都向后一位
(6) 此时又失配了,目前k=1,所以next[10]=1
至此,可以较快完成整个字符串的next值计算。
0x15 next计算规则
next计算的本质上,是后缀子串与最前的子串匹配的过程,要模拟这个过程,只需要添加一个前缀索引就可以了,如上面的k。
k的位置就是前缀子串与后缀子串匹配的长度,当存在失配时,k的位置就是最大子串长度,此时需要将k复位,重新开始下一轮前后缀匹配
一般规则如下(设n为当前匹配串的读取位置,k为最大前缀位置标识):
当p[k]=p[n]时,基于优化方案
next[n] = next[k]
然后开始后移,n=n+1,k=k+1
当p[k]!=p[n],
next[n] = k
并复位k=next[k],开始重新匹配,直到k回到首位字符
0x20 实现
程序计算next时,不能采用口算的办法,需要对匹配串从头到尾扫描一次。
0x21 next计算
next的计算流程整理如下:
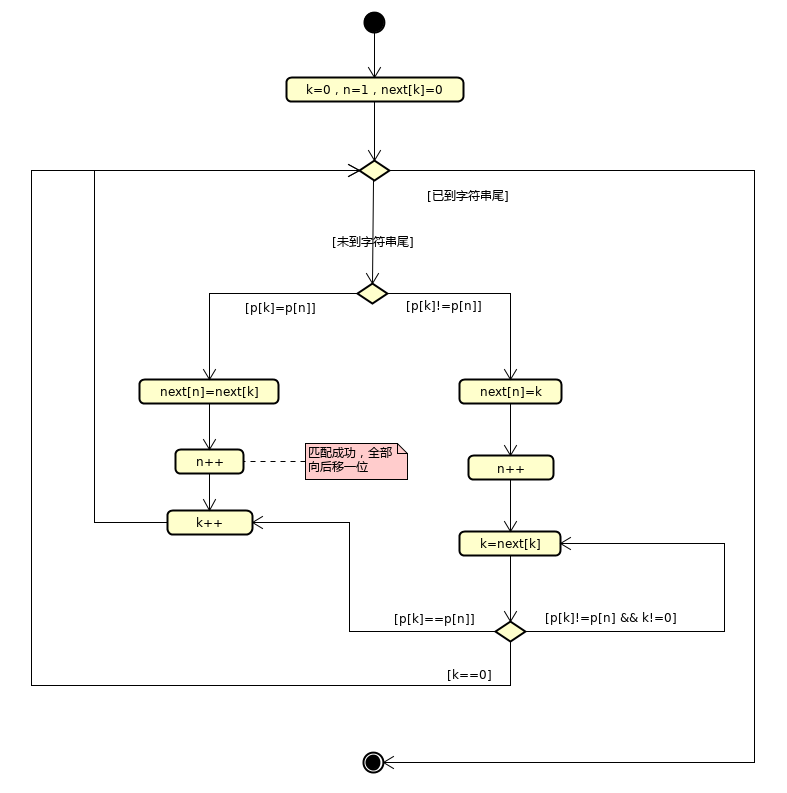
代码示例如下:
1 | void next(char* p,int* next,int length){ |
0x22 字符串匹配
最终才来到匹配的一环,这一步在next出来之后就更简单了,其实就是最开始的暴力破解的变种,直接上代码
1 | int search(char* source,char* p,int* next){ |
其实就是对字符串与匹配串进行一对一的匹配,如果不匹配,则将匹配串的索引j重置为next[j]即可。
如果找到匹配,则返回最终匹配位置。